Solving a Mystery with Cryptography and Python

One cloudy afternoon, while walking down the street, I saw an object tossed out of a speeding car. It was a bag. I was curious to check the contents. The contents looked suspicious, so I quickly snapped some photographs. Little did I know that I was about to embark on a crazy mysterious adventure for the next three days with little to no sleep at all.
Mysteries are always intriguing. So, I was thrilled when I found a ‘stop a bank robbery’ code-breaking challenge on Khan Academy. I have been learning maths from Khan Academy for a long time. Recently, I started learning about Cryptography and came across a fantastic code-breaking challenge. This blog outlines the process of decrypting secret messages with the help of a computer programming language called Python.
Spoiler Alert!
Following this, there are going to be spoilers to the puzzles. So, if you want to solve this on your own, I highly recommend you to go to Khan Academy to solve these puzzles
You may read ahead if you want to read a mystery blog and find out how to do cryptanalysis or are curious about code-breaking.
Chapter 1: The discovery
The contents from the bag thrown out of the car were mysterious. There were blueprints, a circuit diagram, a newspaper clipping, a business card with a hand-written 250 number.



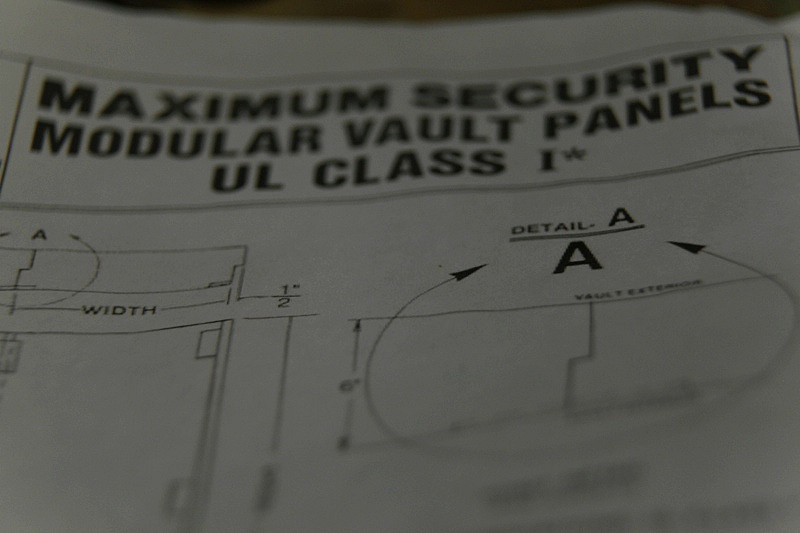
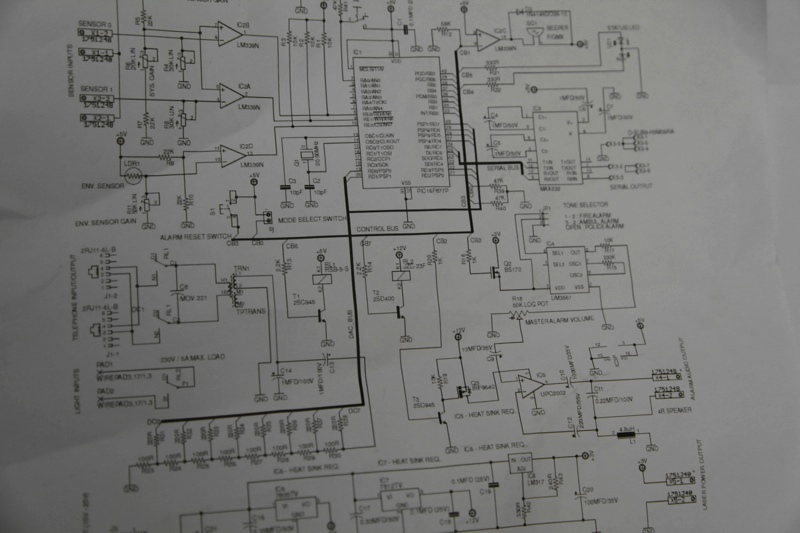


But, one item stood out among the rest. It seemed like a secret code. After returning home, I heard the evening news that said:
Two thieves in their mid-20s are suspected to be in the area; they have been known to strike in neighbouring towns. Just earlier this week, the AMCO insurance office was burglarised and documents were stolen. Reward is being offered for information leading to their arrest…
I realised, to break this code, I must retrace their steps.
Chapter 2: Caesar
The business card looked promising. Luckily, I have a friend who works in Hudson Bay Lodge. I entered that dark hotel. My friend informed me that someone had checked into room 250 for three days. He gave me a copy of the key and told me that I only had two minutes to look.
When I entered the room, I saw a wastebasket with some papers. Luckily, I found clue #1, two encrypted messages.

Transcripts of the above messages:
Message 1:
gluhtlishjrvbadvyyplkoah
avbxjpwolypzavvdlhrvuu
leatlzzhnlzdpajoavcpnl
ulyljpwolyrlfdvykpzaola
pkkluzffivsvmklhaoput
fmhcbypalovsilpuluk
Message 2:
vwduwljudeehghyhubwklq
jlfrxogilqgsohdvhuhwxuq
dqbeoxhsuqwvieuydxowd
qgodupghvljqedvhgrqzk
ifkedqnbrxghflghrqldpvhw
wlqjxsvdihkrxvhfr
Before leaving the hotel, I noticed something else. It looked like an impression from another message. So, I scribbled with a pencil to reveal the hidden text underneath it. The text looked like another cypher.

Message 3:
Klkbnqlcytfysryucocphgbdizz
fcmjwkuchzyeswfogmmetwwossd
chrzyldsbwnydednzwnefydthtd
dbojicemlucdygicczhoadrzcyl
wadsxpilpiecskomoltejtkmqqy
mehpmmjxyolwpeewjckznpccpsv
sxauyodhalmriocwpelwbcniyfx
mwjcemcyrazdqlsomdbfljwnbij
xpddsyoehxpceswtoxwbleecsax
cnuetzywfn
Cracking the code
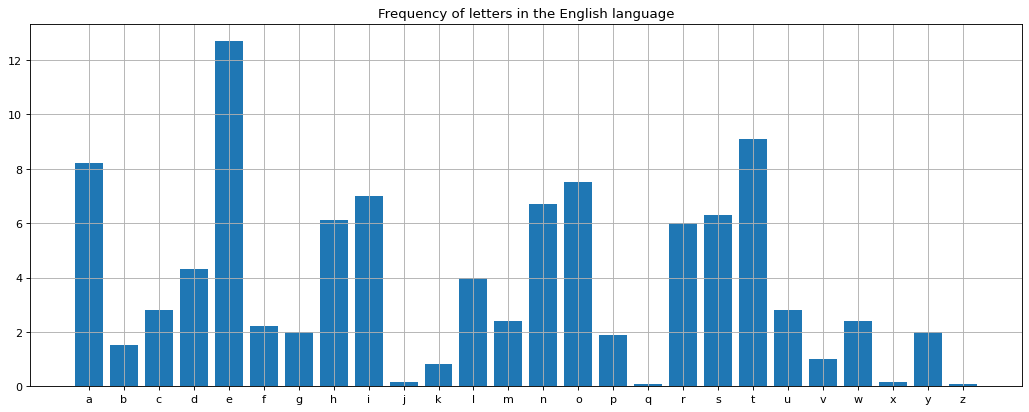
Codebreakers often look for a leak of information. Information leaks can take place in several ways. One way to observe information leak in shifting characters is to observe the frequency of letters, i.e. counting how many times a letter appears in the message.
In the English language, every paragraph has a frequency of letters used. This frequency chart, shown in Fig. 1, acts as a fingerprint. The letter e has the highest frequency. So, when we see an encrypted message, we must find a letter with the highest frequency. The letter with the highest frequency in the encrypted message often corresponds to e. Let us put this theory into practice using the python programming language.
Import necessary python packages
1
2
import copy
import matplotlib.pyplot as plt
Message 1
Let us do a quick frequency analysis of encrypted message 1.
We must first define two functions that will help us count the frequency of letters in the encrypted message.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def char_frequency(message):
"""Takes message as input and returns the frequency of letters as a dictionary"""
freq = dict()
for c in message:
freq[c] = freq.get(c, 0) + 1
return freq
def sort_freq_plot(frequency):
"""Takes a dictionary of frequency as input and returns a sorted dictionary for plotting"""
fr = dict()
alphabets = 'abcdefghijklmnopqrstuvwxyz'
for i in alphabets:
if not i in frequency:
frequency[i] = 0
for i in sorted(frequency):
fr[i] = frequency[i]
return fr
Now, we must plot the frequency graph of the message that will help us find the type of cypher used.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# message 1
message1 = "gluhtlishjrvbadvyyplkoahavbxjpwolypzavvdlhrvuuleatlzzhnlzdpajoavcpnlulyljpwolyrlfdvykpzaolapkkluzffivsvmklhaoputfmhcbypalovsilpuluk"
# Get frequency of letters in the message
freq1 = char_frequency(message1)
fr1 = sort_freq_plot(freq1)
# Plot frequency distribution
plt.figure(figsize=(16,6), dpi=80)
plt.grid()
plt.title("Frequency distribution of message 1")
plt.xlabel("Letters")
plt.ylabel("Number of occurrence")
plt.bar(list(fr1.keys()), list(fr1.values()), align='center')
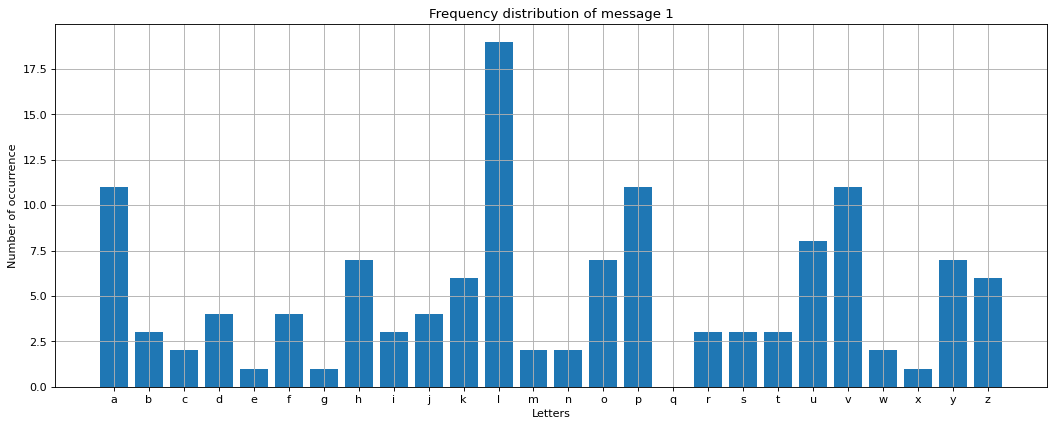
The frequency graph of message 1, shown in Fig. 2, is similar to the frequency graph of any passage in the English language, shown in Fig. 1. We can see that the letter l has the highest frequency of occurrence. When we compare the Fig.1 and Fig. 2, l and e have the largest peaks. Letter l is seven spaces away from e. So, the key must be 7. This encryption is an example of Caesar Cypher, where the messages are encrypted and decrypted using forward and backward shifts, respectively. The following example shows how we encrypt a message by shifting every letter by two spaces to get the encrypted message.
# Using caesar cypher
m: call sherlock
k: 2
e: ecnn ujgtnqem
We can either try using key = 7 or try a brute force approach. In the brute force approach, we try every possible key from 0 to 25 to check for a message that makes sense. You may have a question regarding why go through all the trouble to do frequency analysis? The answer is that we may not be sure whether the encryption was done using Caesar Cypher. Frequency analysis tells us the type of encryption used.
First, we define a decrypting function as follows:
1
2
3
4
5
6
7
def decrypt_caesar(message, key):
"""Takes an encrypted message and the key and returns a decrypted message"""
deciphered = ""
for c in message:
deciphered += chr((ord(c) - ord('a') - key) % 26 + ord('a'))
return deciphered
Then, we execute the function by using the following code:
print(decrypt_caesar(message1, 7))We get the following output:
zenameblackoutworriedhtatouqcipheristooweakonnextmessageswitchtovigenerecipherkeywordisthetiddensyybolofdeathinmyfavuriteholbeinendReorganising the output, we get the first decrypted message. Message 1 is as follows:
ze name blackout worried htat
ouq cipher is too weak
on next message
switch to vigenere cipher
keyword is the tidden syybol of death
in my favurite holbein end
Message 2
Similar to message 1, we must also try frequency analysis on message 2. We can use the following code to get the frequency distribution of message 2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# message 2
message2 = "vwduwljudeehghyhubwklqjlfrxogilqgsohdvhuhwxuqdqbeoxhsuqwvieuydxowdqgodupghvljqedvhgrqzkifkedqnbrxghflghrqldpvhwwlqjxsvdihkrxvhfr"
# Get frequency of letters in the message
freq2 = char_frequency(message2)
fr2 = sort_freq_plot(freq2)
# Plot frequency distribution
plt.figure(figsize=(16,6), dpi=80)
plt.grid()
plt.title("Frequency distribution of message 2")
plt.xlabel("Letters")
plt.ylabel("Number of occurrence")
plt.bar(list(fr2.keys()), list(fr2.values()), align='center')
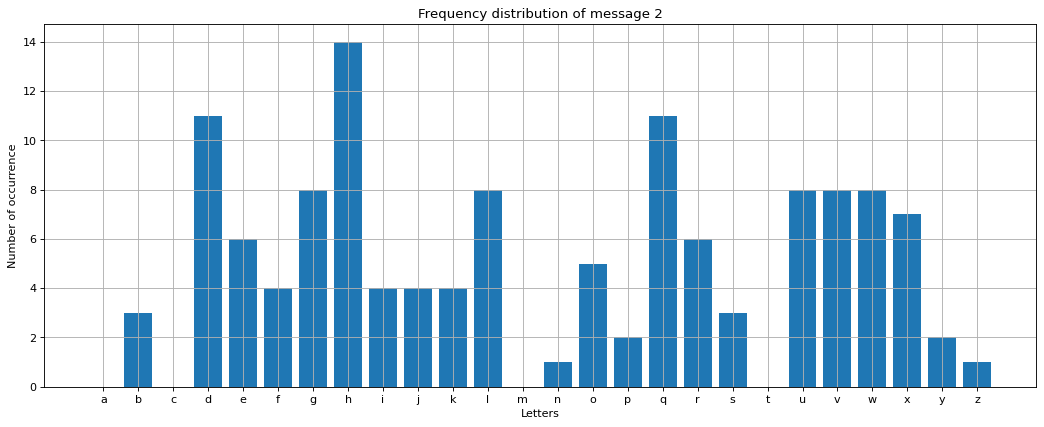
Fig. 3 shows the frequency distribution of message 2. In Fig. 3, h has the highest peak. h is three letters away from e. Therefore, the key must be 3. We can use the following code to decrypt message 2.
print(decrypt_caesar(message2, 3))We get the following output:
startigrabbedeverythingicouldfindpleasereturnanyblueprntsfbrvaultandlarmdesignbasedonwhfchbankyoudecideoniamsettingupsafehousecoNow, we have the decrypted second message as follows:
start i grabbed everything i could find
please return any blueprnts fbr vault and larm
design based on whfch bank you decide on
i am setting up safe house co
Chapter 3: Holbein
The first message from Caesar Cypher talked about the hidden symbol of death in Holbein and switch to vigenere cipher. I searched the Holbein on the internet, and after going through several images, one image struck out. The image was a famous painting by Holbein called The Ambassadors. Fig. 4 shows The Ambassadors by Hans Holbein the Younger.

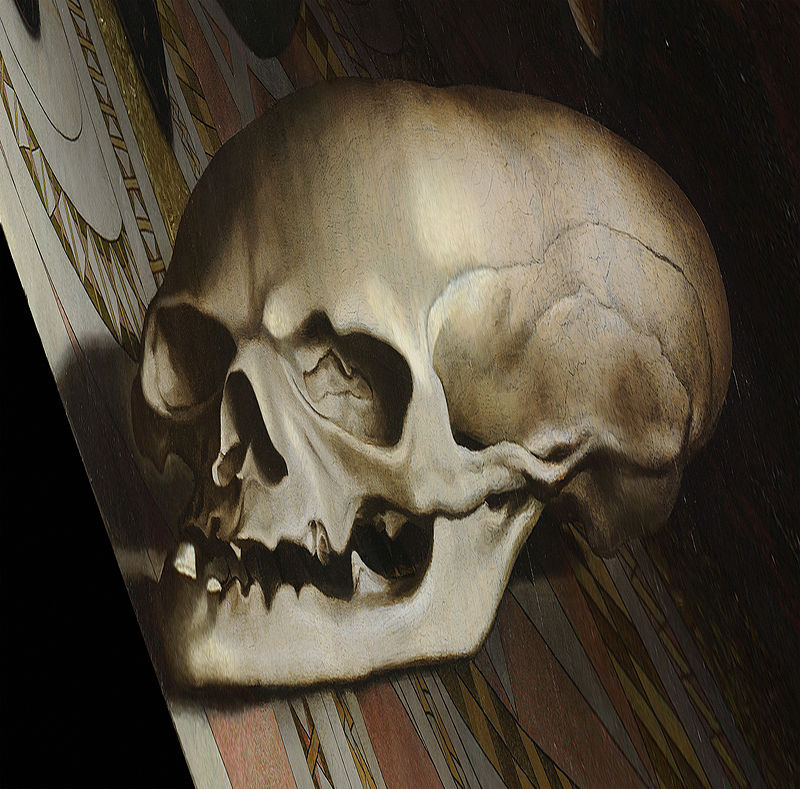
The painting is of two gentlemen standing with many objects in the background. However, there was a weird image at the bottom of the painting. Initially, it seemed like a log of wood. But, upon seeing this image from a different perspective, as seen in Fig. 5, one notices a hidden skull. So, perhaps the word skull is the code word.
Chapter 3: Vigenere
Using the following code, we can plot the frequency distribution of message 3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# message 3
message3 = "klkbnqlcytfysryucocphgbdizzfcmjwkuchzyeswfogmmetwwossdchrzyldsbwnydednzwnefydthtddbojicemlucdygicczhoadrzcylwadsxpilpiecskomoltejtkmqqymehpmmjxyolwpeewjckznpccpsvsxauyodhalmriocwpelwbcniyfxmwjcemcyrazdqlsomdbfljwnbijxpddsyoehxpceswtoxwbleecsaxcnuetzywfn"
# Get frequency of letters in the message
freq3 = char_frequency(message3)
fr3 = sort_freq_plot(freq3)
# Plot frequency distribution
plt.figure(figsize=(16,6), dpi=80)
plt.grid()
plt.title("Frequency distribution of message 3")
plt.xlabel("Letters")
plt.ylabel("Number of occurrence")
plt.bar(list(fr3.keys()), list(fr3.values()), align='center')
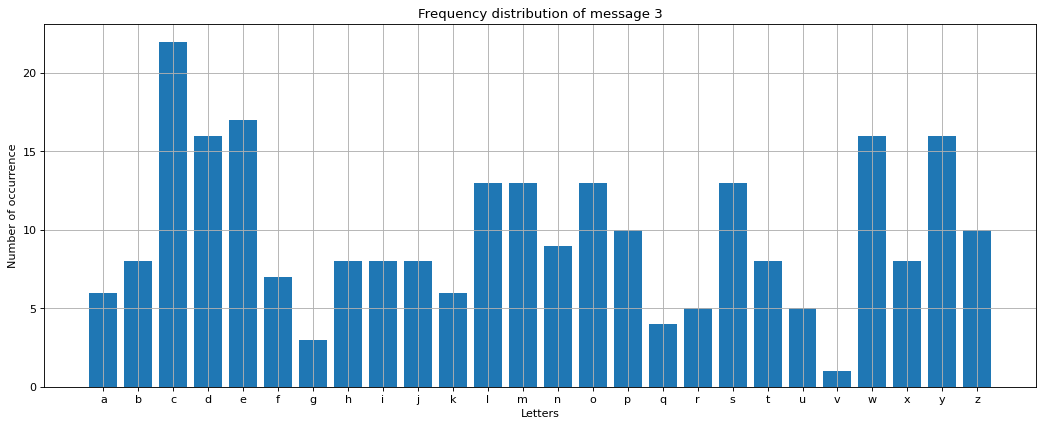
The frequency distribution of message 3, shown in Fig. 6 do not follow a standard pattern, as seen in Fig. 1. We can conclude from the frequency distribution that we cannot use Caesar cypher because it is not a simple shift of all the letters. Each letter seems to have shifted with its key in the third message. However, we are not entirely helpless here. We got some help from message 1 that they will use Vigenere cypher for encryption in their future communications with the secret code word as skull.
Vigenere cypher uses a secret code word where we shift every letter by the key associated with that word. Following is an example of how we encrypt a message call sherlock by using the code word watson to get an encrypted message.
m: call sherlock
s: wats onwatson
e: yaed guardgqx
So, we know which cypher to use and the code word. However, knowing the code word may not be enough to decrypt the message. We are lucky when we know the secret code word skull. But, we still get gibberish when we implement the code word skull to decrypt message 3. Therefore, knowing the code word is not enough; it is also essential to know the length of the code word.
To find the length of the code word, we must find an information leak that often happens in long messages with repeating words. Since we are moving the same code word across the encrypted message, we start seeing peaks in the distribution after a few intervals.
Cracking the code
We shift the message as follows and find the coincidences, i.e. the letters of the shifted message with one letter to the right that matches the original cyphertext. Following is an example of shifting the cyphertext.
ibmiaqpztphflqypu... <-- original cyphertext
ibmiaqpztphflqyp | 0
ibmiaqpztphflqy | 0
ibmiaqpztphflq | 2
ibmiaqpztphfl | 0
ibmiaqpztphf | 0
ibmiaqpztph | 1
ibmiaqpztp | 0
In the above shift of messages, the column on the right shows the number of letters matching the cyphertext. When iterating over the message, we will find peaks at different intervals, and the intervals in between the peaks tell us the length of the word. Though, this is not a perfect method as it only gives you an estimate regarding the length of the word. Sometimes, there may be peaks observed at different locations where you may have to guess.
We can use the following code to find these peaks. First, we need to define two functions that quantify messages to a list of shifting characters and find the coincidence in the quantified messages with the original cyphertext.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def quantify_message(message):
"""Takes the message and returns a list of quantified messages with on right shift"""
d_message = copy.deepcopy(message)
text = list(d_message)
new_messages = []
while text:
text.pop(-1)
new_messages.append("".join(text))
return new_messages
def coincedences(message):
"""Takes a list of messages with one right shift in each message
and finds words that coincide with the main message
"""
count_dict = dict()
loop_iter = 0
repeating_messages = quantify_message(message)
for m in repeating_messages:
count = 0
for i in reversed(message):
for j in reversed(m):
if i == j:
count += 1
m = m[:-1]
break
count_dict[str(loop_iter)] = count
loop_iter += 1
return count_dict
Then, we implement the following code to get the graph of intervals.
1
2
3
4
5
6
7
8
9
10
11
# Using only first 100 characters of the cyphertext
freq_d = coincedences(message3[:100])
# Plotting the graph
plt.figure(figsize=(20,6), dpi=80)
plt.xticks(rotation=90)
plt.grid()
plt.title("Frequency of coincidences")
plt.xlabel("Shifts (Iteration by one shift)")
plt.ylabel("Number of coinciding letters")
plt.bar(list(freq_d.keys()), list(freq_d.values()), align='center')
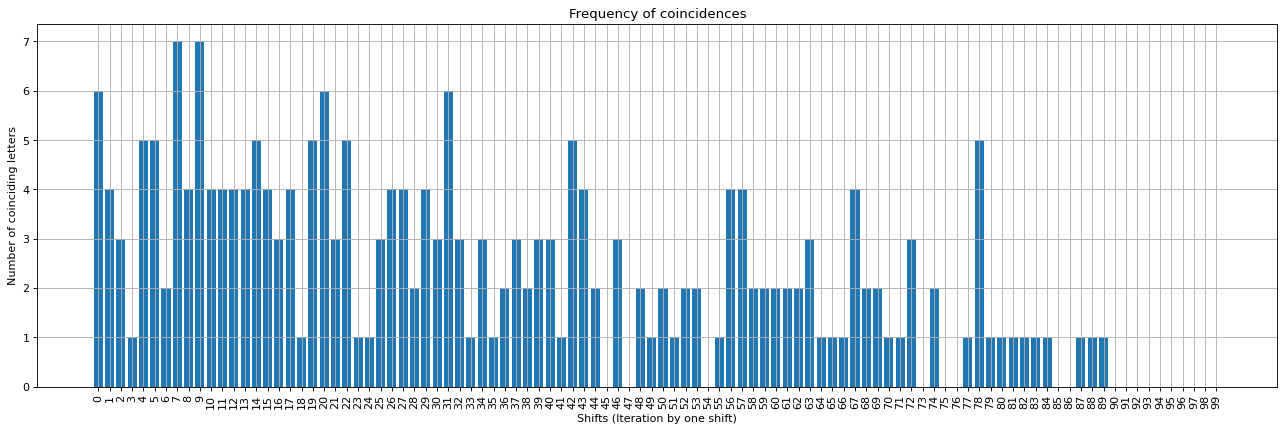
Fig. 7 shows the graph of peak values. The graph is imperfect, but we can see peaks at the 10th intervals. From these peaks, we can determine the length of the codeword is ten. But, skull is a five-letter word. However, if we double the letters, sskkuullll, it becomes the ten-letter secret codeword.
Often, there will be a lot of uneven peaks. Cryptanalysis can sometimes be difficult, and one often needs to guess. Knowing possible lengths can help you guess in the right direction. Also, one needs to resort to trial and error with different combinations of the known keyword.
Use the following code to implement the decryption process of the Vigenere cypher. First we define a function to perform the decryption and then we execute the function to get the decrypted text.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def vigenere_decrypt(message, secret):
"""Takes cyphertext and secret word and returns the plaintext"""
code = []
for c in secret:
code.append(ord(c) - ord('a'))
encoding = []
decrypted = ""
q = len(message) // len(secret)
r = len(message) % len(secret)
encoding = code * q
remaining = code[:r]
encoding.extend(remaining)
for c, e in zip(message, encoding):
decrypted += chr((ord(c) - ord('a') - e) % 26 + ord('a'))
return decrypted
Implement the following function:
1
2
3
# Skull was the hidden symbol of death in Holbein the younger, The Ambassador painting.
secret = "sskkuullll"
print(vigenere_decrypt(message3, secret))
The output of the above code will be as follows:
startwarningiheardreportofourbreakinonthenewsstillwaitingonalarmtestschedulesiwillreportbacktomorrowwithfinalplanforextrasecurityisuggestweburnourlettersafterreadingandswitchourletterstonumbersusingpolybiussquaredropmessageunderthebenchattrainstationendAfter reorganising the output, we get the following message:
start
warning i heard report of our break in on the news
still waiting on alarm test schedules
i will report back tomorrow with final plan
for extra security i suggest we burn our letters after reading
and switch our letters to numbers
using polybius squared rop message
under the bench at train station
end
The critical clue from message 3 is the polybius squared rop message.
Chapter 4: Polybius
After deciphering the first three messages, I took a stroll to the train station. But, I didn’t see anything under the bench, as message 3 pointed out. But then, I glanced at a burnt paper close to the train tracks.

Transcript of the above message:
44541134541123335344541242
43424432514121231131135315
54425442444243443251415343
54324234411125513553341342
43225343114454345343225134
31421432513412533412155415
34513351444411225144425442
44441534512355154321345111
13112123514254315333214243
51445315341434512542531544
335154325341443 (cut off)
43513544
Polybius cypher works on a grid system. The message polybius squared rop makes me wonder if there was a typo. I think they meant top instead of rop. So, we need to make a grid starting from the top.
| 0 | 1 | 2 | 3 | 4 |
--+---+---+---+---+---+
0 | a | f | k | p | u |
--+---+---+---+---+---+
1 | b | g | l | q | v |
--+---+---+---+---+---+
2 | c | h | m | r | w |
--+---+---+---+---+---+
3 | d | i | n | s | x |
--+---+---+---+---+---+
4 | e | j | o | t | y |
--+---+---+---+---+---+
Once we set up the grid, we use two numbers in sequence to encrypt every character. We use 00 to encrypt a, and 44 to encrypt y. Refer to the following example:
+----+----+----+----+----+
m:| h | e | l | l | o |
+----+----+----+----+----+
e:| 21 | 40 | 12 | 12 | 42 |
+----+----+----+----+----+
Cracking the code
We must couple two numbers from the number sequence of message 4 to get the coordinates. We use the coordinates to find the characters from the Polybius square. To accomplish this, we first create the following function:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def polybius(in_message, poly_grid):
"""Takes message and a polybius grid and returns the decrypted message"""
ciphers = []
decrypted = ''
st = ''
# Removing white spaces
for c in in_message:
if c != ' ':
st += c
else:
ciphers.append(st)
st = ''
for cipher in ciphers:
# converting string to int
n = [int(x) for x in cipher]
# creating tuples from the numbers
grid = [x for x in zip(*[iter(n)]*2)]
message = ''
for co_ord in grid:
message += poly_grid[co_ord[0] - 1][co_ord[1] - 1]
# Adding message to decrypted
decrypted += message
return decrypted
Then, we execute the function to get the decrypted message.
1
2
3
4
5
6
7
8
9
10
11
12
# message 4
message4 = "44541134541123335344541242 43424432514121231131135315 54425442444243443251415343 54324234411125513553341342 43225343114454345343225134 31421432513412533412155415 34513351444411225144425442 44441534512355154321345111 13112123514254315333214243 51445315341434512542531544 335154325341443 43513544"
# polybius square
poly = [['a', 'f', 'k', 'p', 'u'],
['b', 'g', 'l', 'q', 'v'],
['c', 'h', 'm', 'r', 'w'],
['d', 'i', 'n', 's', 'x'],
['e', 'j', 'o', 't', 'y']]
# decrypting and printing the message
print(polybius(message4, poly))
We should get the following output:
startalmostfinishedblackoutitisinshedonthirdaveworkingonastrongercipherforfuturemessagesitissurelyunbreakableitcombinesourpreviousmethodsAfter reorganising the output, we get the following message:
start
almost finished blackout
it is in shed on third ave
working on a stronger cipher for future messages
it is surely unbreakable
it combines our previous methods
Chapter 5: Zeros and Ones
Finally, after decoding the first four messages, I learned the safehouse’s location and name (“blackout”). I approached the safehouse. There wasn’t anyone around, so I entered the safehouse. It was a dark place. Luckily, I brought a flashlight and quickly snapped some images.







It seems like the clues that I found in the safehouse has everything to do with the clues that I found from the bag. The clues from the safehouse provide steps to encrypt the message.
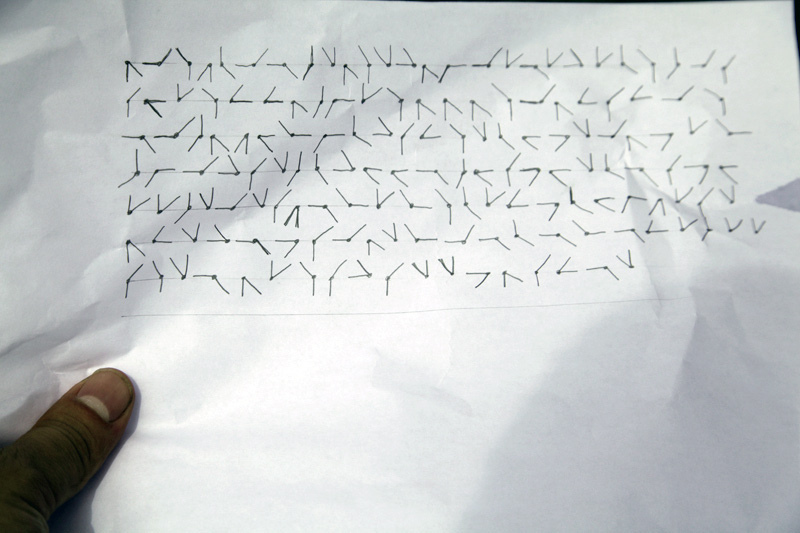
Angles
My first order of business was to decipher the angles. One of the clues from the safehouse pages was about a compass. Also, every angle in the message has a cardinal direction (East, West, North, South) and an intermediate direction (North East, North West, South East, South West). Digging deeper into some pages, I realised that the angles follow a number system that limits up to the number 3. So, I concluded that the angles are as follows:
10 00 11
\ | /
\|/
11---+---01
/|\
/ | \
01 10 00
We can decode the angles with the compass direction and the corresponding binary numbers associated with the direction. First, we must start with the cardinal angle value and take the intermediate angle value. We can decode the angles as follows:
|/ | |/
/
0011 0001 0011

After decoding the compass angles, we can use the image found from the bag in Fig. 8 and decode the message. The message is still a bunch of binary numbers and not much use to us yet. The message from Fig. 8 translates as follows:
1000 1111 1010 1001 0000 1111 1100 0001 0010 1000 1010 0010 1110 1000 0101 1111 0011 1100 0011 1110 0011 0000 1010 0001 1111 1011
1011 0100 0011 1010 0111 0111 1000 0001 0101 0011 1010 1000 1000 1000 1010 1111 1000 0111 1011 0111 1111 1010
1100 1111 0001 1000 1001 0100 0110 0101 0000 1110 1011 0111 1010 0010 0000 0100 1101 0010 1111 1000 1101 0011 1001
0001 0101 1111 1110 1011 0010 0001 0000 1110 0100 0100 1100 0001 0100 1011 1101 0100 0010 0000 1100 1011 1101 0100
0011 0011 0001 0010 1111 0010 1011 1001 1100 0110 0011 0110 1010 0000 0011 0111 1101 0000 0100 0101 1001 0011 1011 0010
1000 0111 0010 1110 1100 1101 1011 1111 1000 0010 0110 1111 1100 0000 1100 0110 1100 0111 0011 0001 0011 0011
1011 1010 0010 1100 1000 0011 1010 1011 1110 1011 0010 0010 1101 1000 1011 0111 1100 0010
I had to decode the angles manually. So, there is a chance of misplacing a number. This misplacement could be a catastrophe.
We must combine the binary digits and eliminate all the white spaces as follows:
1
2
3
4
5
6
7
8
9
10
11
message5 = """1000 1111 1010 1001 0000 1111 1100 0001 0010 1000 1010 0010 1110 1000 0101 1111 0011 1100 0011 1110 0011 0000 1010 0001 1111 1011
1011 0100 0011 1010 0111 0111 1000 0001 0101 0011 1010 1000 1000 1000 1010 1111 1000 0111 1011 0111 1111 1010
1100 1111 0001 1000 1001 0100 0110 0101 0000 1110 1011 0111 1010 0010 0000 0100 1101 0010 1111 1000 1101 0011 1001
0001 0101 1111 1110 1011 0010 0001 0000 1110 0100 0100 1100 0001 0100 1011 1101 0100 0010 0000 1100 1011 1101 0100
0011 0011 0001 0010 1111 0010 1011 1001 1100 0110 0011 0110 1010 0000 0011 0111 1101 0000 0100 0101 1001 0011 1011 0010
1000 0111 0010 1110 1100 1101 1011 1111 1000 0010 0110 1111 1100 0000 1100 0110 1100 0111 0011 0001 0011 0011
1011 1010 0010 1100 1000 0011 1010 1011 1110 1011 0010 0010 1101 1000 1011 0111 1100 0010"""
message5 = message5.replace(" ", "")
message5_str = message5.replace("\n", "")
print(message5_str)
You should get the following output:
10001111101010010000111111000001001010001010001011101000010111110011110000111110001100001010000111111011101101000011101001110111100000010101001110101000100010001010111110000111101101111111101011001111000110001001010001100101000011101011011110100010000001001101001011111000110100111001000101011111111010110010000100001110010001001100000101001011110101000010000011001011110101000011001100010010111100101011100111000110001101101010000000110111110100000100010110010011101100101000011100101110110011011011111110000010011011111100000011000110110001110011000100110011101110100010110010000011101010111110101100100010110110001011011111000010Newspaper
I found a newspaper in the safe house where I observed that every consonant was 0 and vowel was 1. So, the newspaper found in the bag has something to do with the decryption. I learned this with the message from the newspaper that was encrypted as follows:
Brilliant driver
001001100 001010

Following is the transcript of the newspaper:
the whole grain goodness of blue chip dividend stocks has its limits
utility stocks consumer staples pipelines telecoms and
real estate investment trusts have all lost ground over
the past month even while the broader market has been flat
with the bond market signalling an expectation of rising interest
rates the five year rally for steady blue chip dividend payers has
stalled should you be scared if you own a lot of these stocks
either directly or through mutual funds or exchange traded
funds david baskin president of baskin financial services has
a two pronged answer keep your top quality dividend stocks but be
prepared to follow his firms example in trimming holdings in stocks
such as transcanada corp keyera corp and pembina pipeline corp lets
have mr baskin run us through his thinking on dividend stocks which
are a big part of the portfolios his firm puts together
We must encode the text from Fig. 9 to its binary form. We can use the following code to accomplish this task:
We remove the white spaces
1
2
3
4
pad = "the whole grain goodness of blue chip dividend stocks has its limits utility stocks consumer staples pipelines telecoms and real estate investment trusts have all lost ground over the past month even while the broader market has been flat with the bond market signalling an expectation of rising interest rates the five year rally for steady blue chip dividend payers has stalled should you be scared if you own a lot of these stocks either directly or through mutual funds or exchange traded funds david baskin president of baskin financial services has a two pronged answer keep your top quality dividend stocks but be prepared to follow his firms example in trimming holdings in stocks such as transcanada corp keyera corp and pembina pipeline corp lets have mr baskin run us through his thinking on dividend stocks which are a big part of the portfolios his firm puts together"
pa = pad.replace(" ","")
onepad = pa[:len(message5_str)]
Once we have removed the white spaces, we define a function to encode the newspaper text as follows:
1
2
3
4
5
6
7
8
9
10
def pad_to_bin(message):
vowels = {'a', 'e', 'i', 'o', 'u', 'y'}
bin_pad = "0b"
for c in message:
if c in vowels:
bin_pad += "1"
else:
bin_pad += "0"
return bin_pad
We execute the encoding function for the text as follows:
1
2
bin_pad = pad_to_bin(onepad)
print(bin_pad)
We should get the following output:
0b00100101001100110010010001100100101010000100001010001010010101010010000100101000100100101010100101010010001101001011001000100001000010110001000011001010001010001000101000101001001101001001001001100010010000101000100100100100100101001001011010010100100101000101000101011110010010100011010011001001010100011100010001001000110011101001010101111001010100010100100011001001010001100001100010110010001010001001001010010000101001001000101010010010010010100110010010100101001001001010001001101110010011010101010100001000010010010101001010010010010001010001100010010001001000100010000100100010001010101000111010100100010010101010101010001000
XOR
The second step in the encryption process, as shown in Fig. 10 highlighted using padding from a newspaper article to encrypt a binary message. In the second step, we see two binary sets of binary numbers on either side of the encryption. When we look closer, we find that a bitwise XOR operation with the newspaper padding reverts the binary sequence to its pre-encryption state.

Following is an example of bitwise XOR operation:
| A | B | A xor B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Now, if we perform the operation of (A xor B) xor B with get the result back to column A as follows:
| A xor B | B | (A xor B) xor B = A |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
Therefore, performing an xor operation on the final message in the binary sequence with the newspaper padding will result in the pre-encrypted binary sequence. We perform the bitwise XOR operation of the binary sequence from the angles and the newspaper article as follows:
1
2
3
4
5
6
7
8
9
10
11
12
13
# convert the string to binary format
message5_pad = int(bin_pad,2)
# bitwise xor operation
x_message = message5 ^ message5_pad
# Converting to binary format
final_bin = bin(x_message)
# Removing the first two characters that indicate binary 0b
decrypted_pad = str(final_bin)[2:]
print(decrypted_pad)
We should get the following output:
10101010100110100010101110100101100000001110000001100010000010100001110100010110101000100000100010101001100000001000100001010110100010100100001101100010101000000010010110101110100000110110100010101101010110100001110101000001100110100010000100110110100100001000001110100110100110011010010110010110101110101110010101000110100010100101010000110010100001010110100000000010100100100010101110100000110110100010101101010110100100100010101010100101100110100010000100110110100101100010010101000000100000001110101010001010001001101001001001010100100000100010100110100010100110000000110110100001100000010110010110000110100100100001110101001010Once we have decrypted the binary sequence, as per the clues from the safehouse, we must group them in a sequence of three and convert them into decimal numbers as follows:
1
2
3
4
5
6
7
8
9
10
11
12
n_list = []
while decrypted_pad:
n_list.append(decrypted_pad[:3])
decrypted_pad = decrypted_pad[3:]
poly_cipher = []
for n in n_list:
poly_cipher.append(str(int(n, 2)))
poly_cipher_combined = "".join(poly_cipher)
print(poly_cipher_combined)
We should get the following output:
5251505351300340304050350552101052300210255051033052004553501550532550352031504115510203515146454553534521505124145025500051105350155053255110525131504115513045201003524242322225101051505140155030054541511035222
Polybius Spiral
One of the images from the safe house showed a spiral of numbers. Also, there is a spiral on the first step of encryption in Fig. 10. Also, message 4 mentions the use of previous methods. So, we must use a modified version of Polybius square as follows:
| 0 | 1 | 2 | 3 | 4 | 5 |
--+---+---+---+---+---+---+
0 | f | g | h | i | j | k |
--+---+---+---+---+---+---+
1 | e | x | y | z | 0 | l |
--+---+---+---+---+---+---+
2 | d | w | 7 | 8 | 1 | m |
--+---+---+---+---+---+---+
3 | c | v | 6 | 9 | 2 | n |
--+---+---+---+---+---+---+
4 | b | u | 5 | 4 | 3 | o |
--+---+---+---+---+---+---+
5 | a | t | s | r | q | p |
--+---+---+---+---+---+---+
Same as in the Polybius square method, we must now group the decimal number sequence into groups of two to act as coordinates to identify the character in the Polybius square. We define a new Polybius function that handles the input in this case.
1
2
3
4
5
6
7
8
9
10
11
12
13
def polybius2(codes, poly_grid):
grid = [x for x in zip(*[iter(codes)]*2)]
message = ''
for co in grid:
x = int(co[0])
y = int(co[1])
if x > 5 or y > 5:
message += '?'
else:
message += poly_grid[x][y]
return message
We implement the polybius function by executing the following code:
1
2
3
4
5
6
7
8
9
pol4 = [['f', 'g', 'h', 'i', 'j', 'k'],
['e', 'x', 'y', 'z', '0', 'l'],
['d', 'w', '7', '8', '1', 'm'],
['c', 'v', '6', '9', '2', 'n'],
['b', 'u', '5', '4', '3', 'o'],
['a', 't', 's', 'r', 'q', 'p']]
decrypted_message5 = polybius2(poly_cipher_combined, pol4)
print(decrypted_message5)
We should get the following output:
startcibcbankseeschematicsforalarmandvaulthitt?oorrowat10amafteralarmtestvaultcodeis5567meetatblackouten7After reorganising the output, we have the final message.
start
cibc bank see schematics for alarm and vault
hit t?oorrow at 10am after alarm test
vault code is 5567
meet at blackout
en7
The word tomorrow is misspelt in the final message. This error is a good example of how a single bit change can cause major errors. Thankfully, the error is not too large to not figure out what the final message has to say.
Epilogue
I decrypted the secret code, and the police have accepted my information and now acting on it.
Acknowledgement
If it is still not obvious, let me clarify that the above story is fictitious, and any events mentioned above never happened. I am grateful to Khan Academy for this puzzle, which I recently learned, was released in 2014. All the images provided as clues are from Khan Academy, and they deserve full credit for those images.
I accidentally stumbled upon this puzzle while learning cryptography. Some of the puzzles were very difficult for me. Thanks to Khan Academy, I recently learned about the frequency analysis of a message and its role in encryption. I learned several encryption techniques while doing this challenge that I did not know before. I would have been lost without some clues provided by the challenge and the community discussion in the comments.
This blog post is not sponsored by any organisations or companies mentioned here. Khan Academy is a non-profit organisation aiming to create online tools that help educate students, and I greatly appreciate this organisation and their work.
Image credit
Cover photo by alexey turenkov on Unsplash
Clue images provided by Khan Academy